解三角形

解三角形例题I

已知条件

在三角形ABC中：

  1. 内角A, B, C的对边分别为a, b, c
  2. $b^2 = ac$
  3. D在边AC上
  4. $BD \sin \angle ABC = a \sin C$
  5. $AD = 2DC$

求解步骤

  1. 利用已知条件，得到向量关系： $\overrightarrow{BD} = \frac{2}{3}\overrightarrow{BC} + \frac{1}{3}\overrightarrow{BA}$

  2. 整理得到方程： $6a^2 - 11ac + 3c^2 = 0$

  3. 因式分解： $(2a - 3c)(3a - c) = 0$

  4. 解得： $a = \frac{3}{2}c$ 或 $a = \frac{1}{3}c$

  5. 验证哪个解满足三角形边长关系：

    • 当 $a = \frac{3}{2}c$ 时： $b^2 = ac = \frac{3}{2}c^2$，即 $b = c\sqrt{\frac{3}{2}}$ 验证三角形不等式：$a + b > c$，$\frac{3}{2}c + c\sqrt{\frac{3}{2}} > c$ 成立
    • 当 $a = \frac{1}{3}c$ 时： $b^2 = ac = \frac{1}{3}c^2$，即 $b = \frac{c}{\sqrt{3}}$ 验证三角形不等式：$a + b = \frac{1}{3}c + \frac{c}{\sqrt{3}} \approx 0.91c < c$，不成立

  6. 确定正确的边长关系：$a = \frac{3}{2}c$，$b = c\sqrt{\frac{3}{2}}$

  7. 使用余弦定理计算 $\cos \angle ABC$： $\cos B = \frac{a^2 + c^2 - b^2}{2ac}$

  8. 代入已知关系： $\cos B = \frac{(\frac{3}{2}c)^2 + c^2 - (\frac{3}{2}c^2)}{2 \cdot \frac{3}{2}c \cdot c} = \frac{\frac{9}{4}c^2 + c^2 - \frac{3}{2}c^2}{3c^2} = \frac{\frac{7}{4}c^2}{3c^2} = \frac{7}{12}$

结论

$\cos \angle ABC = \frac{7}{12}$

解三角形例题II

如图,在平面四边形 $ABCD$ 中, $\angle ABC = \theta$ ($0 < \theta < \pi$), $AB = BC = CD = 1$, $AC\perp CD$。

图示1

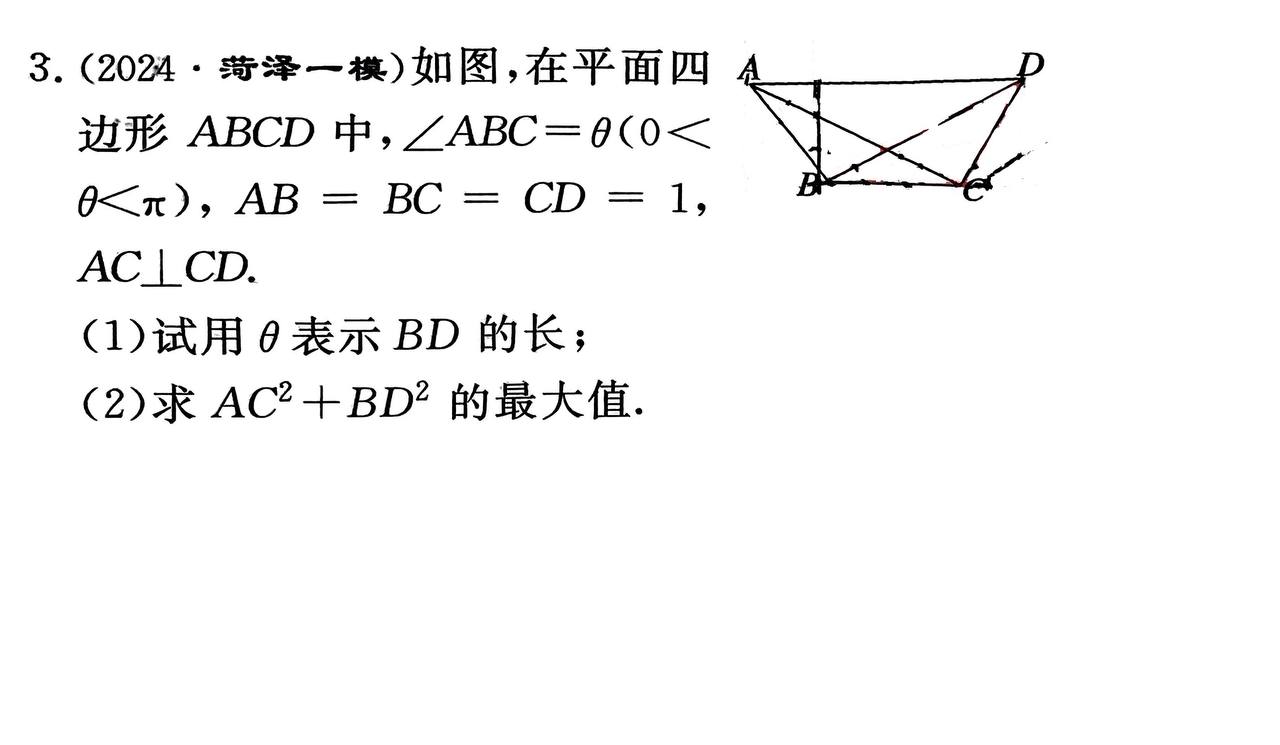
(1) 试用 $\theta$ 表示 $BD$ 的长; (2) 求 $AC^2 + BD^2$ 的最大值。

(1) 用 $\theta$ 表示 $BD$ 的长度

根据图片中的解法:

$$ \begin{align*} \angle ACB &= \frac{\pi - \theta}{2} \ \therefore \angle CBD &= \frac{\pi + \theta}{2} + \angle ACB = \pi - \frac{\theta}{2} \ \therefore \angle CBD &= \boxed{\frac{\theta}{2}} \end{align*} $$

由于 $CD = 1$, 我们可以得到:

$$ \begin{align*} \frac{BD}{\sin\left(\pi - \frac{\theta}{2}\right)} &= \frac{1}{\sin\frac{\theta}{2}} \ \therefore BD &= \boxed{2\cos\frac{\theta}{4}} \end{align*} $$

(2) 求 $AC^2 + BD^2$ 的最大值

已知 $AC^2 = 2 - 2\cos\theta$, 将 $BD$ 的表达式代入:

$$ \begin{align*} AC^2 + BD^2 &= 2 - 2\cos\theta + 4\cos^2\frac{\theta}{4} \ &= 2 - 2\cos\theta + 2 + 2\cos\frac{\theta}{2} \ &= 4 - 2\cos\theta + 2\cos\frac{\theta}{2} \end{align*} $$

设 $x = \frac{\theta}{2}$, $0 < x < \frac{\pi}{2}$, 则:

$$ \begin{align*} AC^2 + BD^2 &= 4 - 2\cos2x + 2\cos x \ &= 4 - 4\cos^2x + 2\cos x \ &= 6 - 4\cos^2x + 2\cos x \end{align*} $$

令 $y = \cos x$, 则 $0 < y < 1$, 上式可以写作:

$$ f(y) = 6 - 4y^2 + 2y $$

这是一个关于 $y$ 的二次函数。由于二次项系数为负, $f(y)$ 的最大值出现在 $y = \frac{1}{4}$ 时:

$$ \begin{align*} f\left(\frac{1}{4}\right) &= 6 - 4\left(\frac{1}{4}\right)^2 + 2\left(\frac{1}{4}\right) \ &= 6 - 1 + \frac{1}{2} \ &= \boxed{\frac{25}{4}} \end{align*} $$

因此, $AC^2 + BD^2$ 的最大值为 $\frac{25}{4}$。